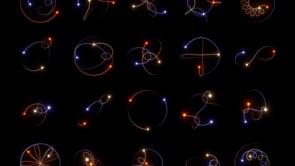
ANSTO scientist Dr Pablo Galaviz undertook his PhD on the three body problem as it applies to black holes. He has written a two-part series on the topic. Part 1 explains the concept and provides historical context.
Recently, the three-body problem has attracted the imagination of the general public thanks to a science fiction TV series on Netflix based on the trilogy The Three-Body Problem by Chinese author Liu Cixin.

The title refers to the classical three-body problem, a fascinating intellectual puzzle relating to the motion of three celestial bodies under their mutual Newtonian gravitational attraction. It is one of many scientific problems where a slight generalisation of a simple system results in a challenging problem.
The two-body problem reduces to a one-dimensional single-particle movement by choosing a convenient coordinate system. The equations of motion of the reduced problem have a closed-form solution. On the other hand, for the three-body problem, only in a few cases can the equations of motion be reduced simply enough to obtain an analytical solution.
The main plot of the series involves an alien civilisation that inhabits a planet in the nearby star system, Alpha Centauri. In the story, the planet endures extreme climate change due to the chaotic nature of the triple star system. In reality, a triple system with chaotic properties would quickly encounter two possible outcomes. In the first scenario, two of the stars collide, forming a giant star or, in some cases, a neutron star or black hole, depending on the mass of the stars. The second possibility is that one of the stars is ejected from the system, leaving a binary system.
Insights for the more technically-minded reader
Alpha Centauri is indeed a triple hierarchical system consisting of Alpha Centauri A, B, and C. Alpha Centauri A is a sun-like star slightly heavier than the sun (1.1 solar masses). Alpha Centauri B is its companion binary of around 0.9 solar mass. This inner system orbits around a common centre of mass with a maximum separation equivalent to the distance between Pluto and the Sun, at their minimum separation equivalent to the one between Saturn and the Sun. Although gravitationally bounded, Alpha Centauri C is far from the binary system. Its separation is equivalent to about 430 times the radius of Neptune's orbit. Alpha Centauri C, or Proxima Centauri, hosts two planets. No known planets are orbiting the binary system. If such planets exist, we should find them in a stable orbit near one of the stars.
History of the three-body problem
The three-body problem, a subject of great historical significance, has catalysed the development of new mathematical ideas and methods. The early attempts to solve the problem started around 1687 when Issac Newton published his book Principia and geometrically solved the problem of two bodies. Newton tried without success to describe the orbits of the moon, earth and sun using the same techniques.
Between 1748 and 1772, Leonhard Euler studied the restricted problem in which the third body, assumed to have no mass, moves in the plane defined by the two revolving bodies. While gravitationally influenced by them, it exerts no influence of its own.
Euler found a particular solution in which the three bodies stay in a line (collinear configuration) and whose properties do not change over time.
Joseph-Louis Lagrange found in 1772 a particular solution where the three bodies are placed at the corners of an equilateral triangle. Studying the restricted problem, Lagrange found five unique points where the forces acting on the third body of a rotating system are balanced. The “Lagrangian points” are important because they are stable orbits for satellites.
The classical period of the three-body problem culminated with the work of Henri Poincaré. In 1890, Poincaré published a memoir on the restricted three-body problem, a reviewed version of the original work that won Oscar II, King of Sweden's mathematical competition. Poincaré's memoir goes beyond the three-body problem. It deals for the first time with the qualitative theory of dynamical systems.
In 1912, Karl F. Sundman solved the problem mathematically by providing a convergent power series solution valid for all time values. However, the convergence rate of the series is extremely slow and useless for practical purposes. Between 1750 and the beginning of the 20th century, more than 800 papers relating to the three-body problem were published.
Since 1950, computational numerical simulations of the three-body problem have provided the best approximation to the solution for a given initial configuration. Numerical solutions to the n−body problem do not distinguish between two, three, or more bodies because the same technique works in each case. The only difficulty arises from the fact that the computational cost increases with the inclusion of more bodies into the problem.
Part 2 explores the role of chaos and the relevance of the three body problem at ANSTO.